Tensorflow 学习笔记
1. 基础概念
1.1 人工智能
人工智能:让机器具备人的 思维 和意识
人工智能三学派:
行为主义:基于控制论,构建感知—动作控制系统。(如汽车的自动驾驶)
符号主义:基于数学逻辑表达式,人为发现规律,把问题描述为表达式,理性思维的实现。
连接主义:仿生学,模仿神经元连接关系,实现感性思维。(比如今天见到陌生人 A,明天再见就会感到眼熟)
深度学习——神经网络————> 连接主义
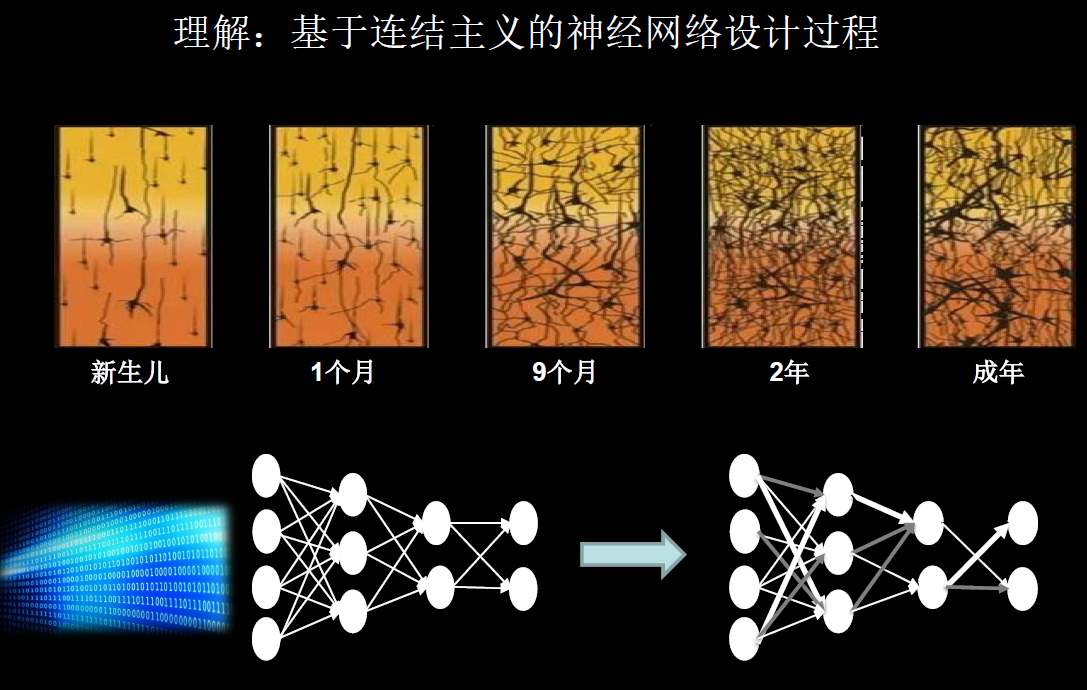
利用仿生学的观点,用计算机仿出神经网络连接关系,让计算机具备感性思维
1.2 神经网络实现思路
- 准备数据:采集大量“特征 / 标签”数据对。
- 搭建网络:搭建神经网络结构。
- 优化参数:训练网络获取最佳参数。
- 应用网络:将网络保存为模型,输入新数据,输出分类或预测结果。
1.3 一些名词解释
损失函数:预测值(y)与标准答案(y_)的差距。
损失函数可以定量判断 w,b 的优劣,当损失函数输出最小时,参数 w,b 会出现最优值。
常用均方误差 MSE 代表损失函数。
$$
MSE(x,y)=∑((y-y_)^2)/n
$$
$$
loss_mse=tf.reduce_mean(tf.square(y_-y))
$$
优化参数:找到一组参数 w,b,使得损失函数最小。
梯度:损失函数对各参数求偏导后的向量。
梯度下降法:沿损失函数梯度下降的方向,寻找损失函数的最小值,得到最优参数的方法。
w 的更新:
$$
w_{t+1}=w_t-l_r×\frac{∂loss}{∂w_t}
$$
学习率(lr):当学习率设置过小时,收敛将变得十分缓慢。当过大时,梯度可能在最小值附近来回震荡,甚至可能无法收敛。

指数衰减学习率:先用较大的学习率,快速得到较优的解,然后逐步减小学习率,使模型在训练后期稳定。
指数衰减学习率 = 初始学习率×学习率衰减率 ^(当前轮数 / 多少轮衰减一次)
反向传播:从后向前,逐层求损失函数对每层神经元参数的偏导数,迭代更新所有参数。
举个例子
损失函数
$$
loss=(w+1)^2 \qquad ——>
\frac{∂loss}{∂w}=2w+2
$$
程序的实现:
import tensorflow as tf
w=tf.Variable(tf.constant(5,dtype=tf.float32)) // 随机初始化 w
lr=0.2
epochs=40
for epoch in range(epochs):
with tf.GradientTape() as tape:
loss=tf.square(w+1)
grads=tape.gradient(loss,w)
w.assign_sub(lr*grads)
print('After %s epoch,w is %f,loss is %f'%(epoch,w.numpy(),loss))张量(Tensor):多维数组
标量(scalar):a=0
向量(vector):b=[0,1,2]
矩阵(matrix):c=[[0,1,2],[3,4,5]]
张量(tensor):d=[[[…..]]]
以上可统称张量。
1.4 常用函数
1.4.1 创建张量
tf.constant(张量内容,dtype= 数据类型(可选))
如tf.constant([1,5], dtype= 数据类型(可选))
tf.convert_to_tensor(numpy 数组,dtype= 数据类型)
1.4.2 创建特殊张量
tf.zeros(维度) // 创建全为 0 的张量
tf.ones(维度) // 创建全为 1 的张量
tf.fill(维度,指定值) // 创建全为指定值的张量
tf.random.normal(维度,mean= 均值,stddev= 标准差)
tf.random.uniform(维度,minval= 最小值,maxval= 最大值)1.4.3 统计
tf.cast(张量名,dtype= 数据类型) 类型转换
tf.reduce_min(张量名) 计算张量维度上元素的最小值
tf.reduce_max(张量名) 计算张量维度上元素的最大值
tf.reduce_mean(张量名,axis= 操作轴 0 or 1)
tf.reduce_sum(张量名,axis= 操作轴 0 or 1)1.4.4 可训练
tf.Variable() 将变量标记为可训练
w=tf.Variable(tf.random.normal([2,2],mean=0,stddev=1))以上就是神经网络默认起始 w 的生成方法示例。
1.4.5 数学运算
四则运算:tf.add,tf.subtract,tf.multiply,tf.divide
平方、次方与开方:tf.square,tf.pow,tf.sqrt
矩阵乘:tf.matmul
1.4.6 数据集的构建(重要)
data=tf.data.Dataset.from_tensor_slices((输入标签,标签))1.4.7 独热编码
tf.one_hot(待转换的数据,depth= 几分类)如:
import tensorflow as tf
lables=tf.constant([1,0,2])
output=tf.one_hot(lables,3)
print(output)
输出结果如下:
tf.Tensor([[0. 1. 0.]
[1. 0. 0.]
[0. 0. 1.]], shape=(3, 3), dtype=float32)1.4.8 柔性最大值
tf.nn.softmax(x) 使输出符合概率分布
$$
Softmax(y_i)=\frac{e^{y_i}}{∑e^{y_i}}
$$
1.4.9 获取最大索引
tf.argmax(张量名,axis= 操作轴)
1.5 手动搭建神经网络
以鸢尾花分类为例,它有四个特征值(花瓣长,花瓣宽,花萼长,花萼宽),这四个特征值表现了三种鸢尾花类型。
# 利用鸢尾花数据集,实现前向传播、反向传播,可视化 loss 曲线
# 导入所需模块
import tensorflow as tf
from sklearn import datasets
from matplotlib import pyplot as plt
import numpy as np
# 导入数据,分别为输入特征和标签
x_data = datasets.load_iris().data
y_data = datasets.load_iris().target
# 随机打乱数据(因为原始数据是顺序的,顺序不打乱会影响准确率)
# seed: 随机数种子,是一个整数,当设置之后,每次生成的随机数都一样(为方便教学,以保每位同学结果一致)
np.random.seed(116) # 使用相同的 seed,保证输入特征和标签一一对应
np.random.shuffle(x_data)
np.random.seed(116)
np.random.shuffle(y_data)
tf.random.set_seed(116)
# 将打乱后的数据集分割为训练集和测试集,训练集为前 120 行,测试集为后 30 行
x_train = x_data[:-30]
y_train = y_data[:-30]
x_test = x_data[-30:]
y_test = y_data[-30:]
# 转换 x 的数据类型,否则后面矩阵相乘时会因数据类型不一致报错
x_train = tf.cast(x_train, tf.float32)
x_test = tf.cast(x_test, tf.float32)
# from_tensor_slices 函数使输入特征和标签值一一对应。(把数据集分批次,每个批次 batch 组数据)
train_db = tf.data.Dataset.from_tensor_slices((x_train, y_train)).batch(32)
test_db = tf.data.Dataset.from_tensor_slices((x_test, y_test)).batch(32)
# 生成神经网络的参数,4 个输入特征故,输入层为 4 个输入节点;因为 3 分类,故输出层为 3 个神经元
# 用 tf.Variable()标记参数可训练
# 使用 seed 使每次生成的随机数相同(方便教学,使大家结果都一致,在现实使用时不写 seed)
w1 = tf.Variable(tf.random.truncated_normal([4, 3], stddev=0.1, seed=1))
b1 = tf.Variable(tf.random.truncated_normal([3], stddev=0.1, seed=1))
lr = 0.1 # 学习率为 0.1
train_loss_results = [] # 将每轮的 loss 记录在此列表中,为后续画 loss 曲线提供数据
test_acc = [] # 将每轮的 acc 记录在此列表中,为后续画 acc 曲线提供数据
epoch = 500 # 循环 500 轮
loss_all = 0 # 每轮分 4 个 step,loss_all 记录四个 step 生成的 4 个 loss 的和
# 训练部分
for epoch in range(epoch): #数据集级别的循环,每个 epoch 循环一次数据集
for step, (x_train, y_train) in enumerate(train_db): #batch 级别的循环 ,每个 step 循环一个 batch
with tf.GradientTape() as tape: # with 结构记录梯度信息
y = tf.matmul(x_train, w1) + b1 # 神经网络乘加运算
y = tf.nn.softmax(y) # 使输出 y 符合概率分布(此操作后与独热码同量级,可相减求 loss)
y_ = tf.one_hot(y_train, depth=3) # 将标签值转换为独热码格式,方便计算 loss 和 accuracy
loss = tf.reduce_mean(tf.square(y_ - y)) # 采用均方误差损失函数 mse = mean(sum(y-out)^2)
loss_all += loss.numpy() # 将每个 step 计算出的 loss 累加,为后续求 loss 平均值提供数据,这样计算的 loss 更准确
# 计算 loss 对各个参数的梯度
grads = tape.gradient(loss, [w1, b1])
# 实现梯度更新 w1 = w1 - lr * w1_grad b = b - lr * b_grad
w1.assign_sub(lr * grads[0]) # 参数 w1 自更新
b1.assign_sub(lr * grads[1]) # 参数 b 自更新
# 每个 epoch,打印 loss 信息
print("Epoch {}, loss: {}".format(epoch, loss_all/4))
train_loss_results.append(loss_all / 4) # 将 4 个 step 的 loss 求平均记录在此变量中
loss_all = 0 # loss_all 归零,为记录下一个 epoch 的 loss 做准备
# 测试部分
# total_correct 为预测对的样本个数, total_number 为测试的总样本数,将这两个变量都初始化为 0
total_correct, total_number = 0, 0
for x_test, y_test in test_db:
# 使用更新后的参数进行预测
y = tf.matmul(x_test, w1) + b1
y = tf.nn.softmax(y)
pred = tf.argmax(y, axis=1) # 返回 y 中最大值的索引,即预测的分类
# 将 pred 转换为 y_test 的数据类型
pred = tf.cast(pred, dtype=y_test.dtype)
# 若分类正确,则 correct=1,否则为 0,将 bool 型的结果转换为 int 型
correct = tf.cast(tf.equal(pred, y_test), dtype=tf.int32)
# 将每个 batch 的 correct 数加起来
correct = tf.reduce_sum(correct)
# 将所有 batch 中的 correct 数加起来
total_correct += int(correct)
# total_number 为测试的总样本数,也就是 x_test 的行数,shape[0]返回变量的行数
total_number += x_test.shape[0]
# 总的准确率等于 total_correct/total_number
acc = total_correct / total_number
test_acc.append(acc)
print("Test_acc:", acc)
print("--------------------------")
# 绘制 loss 曲线
plt.title('Loss Function Curve') # 图片标题
plt.xlabel('Epoch') # x 轴变量名称
plt.ylabel('Loss') # y 轴变量名称
plt.plot(train_loss_results, label="$Loss$") # 逐点画出 trian_loss_results 值并连线,连线图标是 Loss
plt.legend() # 画出曲线图标
plt.show() # 画出图像
# 绘制 Accuracy 曲线
plt.title('Acc Curve') # 图片标题
plt.xlabel('Epoch') # x 轴变量名称
plt.ylabel('Acc') # y 轴变量名称
plt.plot(test_acc, label="$Accuracy$") # 逐点画出 test_acc 值并连线,连线图标是 Accuracy
plt.legend()
plt.show()1.6 神经网络(NN)复杂度
NN 层数 +NN 参数个数表示。

空间复杂度:
层数 = 隐藏层的层数 +1 个输出层
总参数 = 总 w+ 总 b
上图示例中层数为 2,总参数为(3×4+4)+(4×2+2)=26
时间复杂度
乘加运算次数
上图中,时间复杂度为(3×4)+(4×2)=20
1.7 激活函数
激活函数的目的:增加网络的非线性分割能力
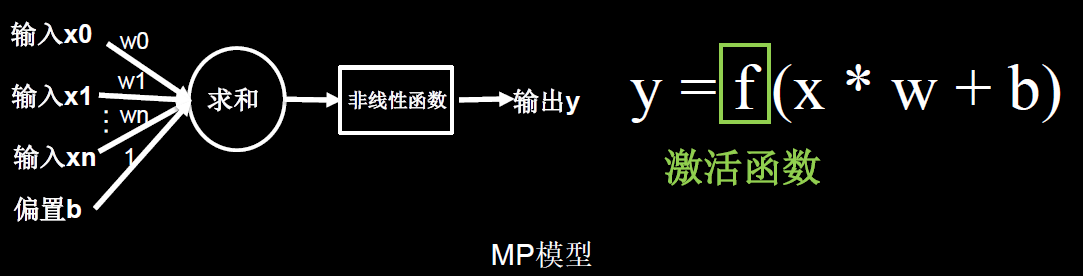

(1)Sigmoid 函数tf.nn.sigmoid(x)
$$
f(x)=\frac{1}{1+e^{-x}}
$$
特点:
易造成梯度消失输出非 0 均值,收敛慢
幂运算复杂,训练时间长
(2)Tanh 函数tf.math.tanh(x)
$$
f(x)=\frac{1-e^{-2x}}{1+e^{-2x}}
$$
特点:
输出是 0 均值
易造成梯度消失
幂运算复杂,训练时间长
(3)Relu 函数tf.nn.relu(x)
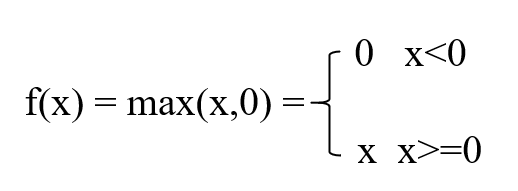
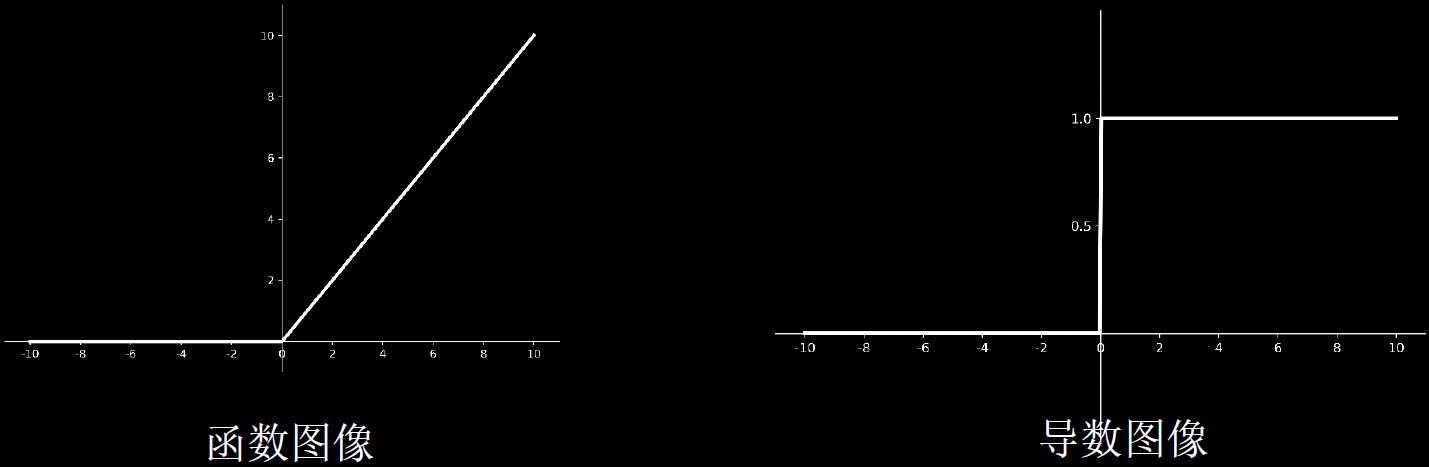
优点:
解决了梯度消失的问题(在正区间)
只需判断输入是否大于 0,计算速度快
收敛速度远快于 sigmoid 和 tanh
缺点
输出非 0 均值,收敛慢
Dead Relu 问题,某些神经元可能永远不被激活,导致相应的参数永远不能被更新。
(4)Leaky Relu 函数tf.nn.leaky_relu(x)

几点认知
首选 relu 激活函数
学习率设置较小值
输入特征标准化,即让输入特征满足以 0 为均值,1 为标准差的正态分布
初始参数中心化,即让随机生成的参数满足以 0 为均值,sqar(2/ 当前层输入特征个数)
1.8 损失函数
1.3 章节已对损失函数做了简单介绍,这里进行补充。均方误差示例代码如下:
import tensorflow as tf
import numpy as np
SEED = 23455
rdm = np.random.RandomState(seed=SEED) # 生成 [0,1) 之间的随机数
x = rdm.rand(32, 2)
y_ = [[x1 + x2 + (rdm.rand() / 10.0 - 0.05)] for (x1, x2) in x] # 生成噪声[0,1)/10=[0,0.1); [0,0.1)-0.05=[-0.05,0.05)
x = tf.cast(x, dtype=tf.float32)
w1 = tf.Variable(tf.random.normal([2, 1], stddev=1, seed=1))
epoch = 15000
lr = 0.002
for epoch in range(epoch):
with tf.GradientTape() as tape:
y = tf.matmul(x, w1)
loss_mse = tf.reduce_mean(tf.square(y_ - y))
grads = tape.gradient(loss_mse, w1)
w1.assign_sub(lr * grads)
if epoch % 500 == 0:
print("After %d training steps,w1 is " % (epoch))
print(w1.numpy(), "\n")
print("Final w1 is: ", w1.numpy())除了采用均方差作为损失函数,还可采用交叉熵作为损失函数
交叉熵损失函数 CE(Cross Entropy):表征两个概率分布之间的距离
$$
H(y_, y)=-∑y_×lny
$$tf.losses.catagorical_crossentropy(y_, y)
softmax 与交叉熵结合:
输出先过 softmax 函数,再计算 y 与 y_的交叉熵损失函数。
tf.nn.softmax_cross_entropy_with_logits(y_, y)
# softmax 与交叉熵损失函数的结合
import tensorflow as tf
import numpy as np
y_ = np.array([[1, 0, 0], [0, 1, 0], [0, 0, 1], [1, 0, 0], [0, 1, 0]])
y = np.array([[12, 3, 2], [3, 10, 1], [1, 2, 5], [4, 6.5, 1.2], [3, 6, 1]])
y_pro = tf.nn.softmax(y)
loss_ce1 = tf.losses.categorical_crossentropy(y_,y_pro)
loss_ce2 = tf.nn.softmax_cross_entropy_with_logits(y_, y)
print(' 分步计算的结果:\n', loss_ce1)
print(' 结合计算的结果:\n', loss_ce2)
// 输出结果是一样的1.9 欠拟合和过拟合
欠拟合:模型不能有效拟合数据集,是对现有数据集学习的不够彻底
过拟合:模型对当前数据拟合的太好了,但对未见过的新数据难以做出正确的判断,模型缺乏泛化力。
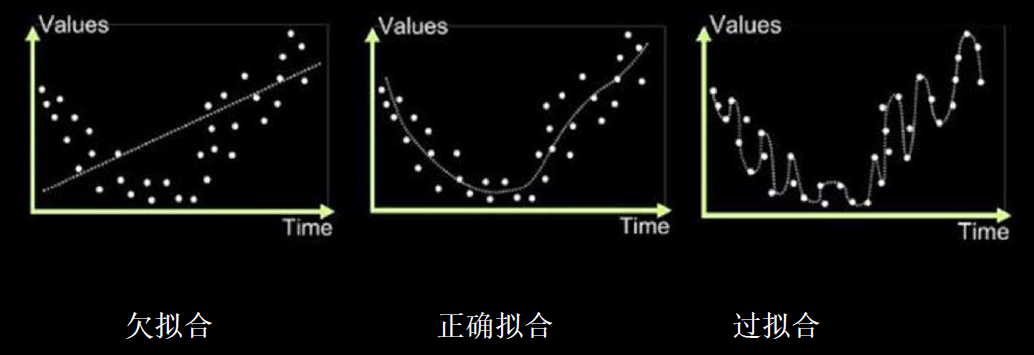
欠拟合解决办法
增加输入特征项
增加网络参数
减少正则化参数
过拟合的解决办法:
数据清洗
增大训练集
采用正则化
增大正则化参数
(1)正则化缓解过拟合
正则化在损失函数中引入模型复杂度指标,利用给 w 加权值,弱化了训练数据的噪声(一般不正则化 b)

正则化的选择:
L1 正则化 大概率会使很多参数变为 0,因此该方法可通过稀疏参数,即减少参数的数量,降低复杂度。
$$
loss_{L1}(w)=∑|w_i|
$$tf.keras.regularizers.l1()
L2 正则化 会使参数很接近 0 但不为 0,因此该方法可通过减少参数值的大小降低复杂度。
$$
loss_{L2}(w)=∑|{w_i}^2|
$$tf.keras.regularizers.l2()
1.10 优化器
神经网络模型中有多种优化算法,优化算法的作用用来优化更新参数 w。
待优化参数 w 每迭代一个 batch(一小段):就会有如下思考:
a. 计算该时刻(t)损失函数关于当前参数的梯度:
$$
g_t=▽loss=\frac{∂loss}{∂(w_t)}
$$
—— t 表示当前 batch 迭代的总次数。b. 计算 t 时刻一阶动量 m
t和二阶动量 Vtc. 计算 t 时刻下降梯度:η
t=lr×mt/√(Vt)d. 计算 t+1 时刻参数:w
t+1=wt-ηt=wt-lr×mt/√(Vt)
一阶动量:与梯度相关的函数
二阶动量:与梯度平方相关的函数
| 动量的释义 |
|---|
| 动量(momentum)来自物理类比,根据牛顿运动定律,负梯度是移动参数空间中粒子的力。 动量在物理学上定义为质量乘以速度。在动量学习算法中,我们假设是单位质量,因此速度向量 v 也可以看作是粒子的动量。 |
| 在某个参数值附近,有一个局部极小点(local minimum):在这个点附近,向左移动和向右移动都会导致损失值增大。如果使用小学习率的 SGD 进行优化,那么优化过程可能会陷入局部极小点,导致无法找到全局最小点。 使用动量方法可以避免这样的问题,这一方法的灵感来源于物理学。有一种有用的思维图像,就是将优化过程想象成一个小球从损失函数曲线上滚下来。如果小球的动量足够大,那么它不会卡在峡谷里,最终会到达全局最小点。 动量方法的实现过程是每一步都移动小球,不仅要考虑当前的斜率值(当前的加速度),还要考虑当前的速度(来自于之前的加速度)。这在实践中的是指,更新参数 w 不仅要考虑当前的梯度值,还要考虑上一次的参数更新。 |
常见优化器如下
(1)随机梯度下降法 SGD:无动量
$$
m_t=g_t
$$
$$
V_t=1
$$
$$
w_{t+1}=w_t-lr×g_t
$$
这里:
$$
g_t=\frac{∂loss}{∂w_t}
$$
参数 w1 自更新:w1.assign_sub(lr×grads[0])
参数 b 自更新:b.assign_sub(lr×grads[1])
(2)SGDM(含动量的 SGD),在 SGD 基础上增加一阶动量
$$
m_t=β·m_{t-1}+(1-β)·g_t
$$
$$
V_t=1
$$
$$
w_{t+1}=w_t-ηt=w_t-lr·(β·m{t-1}+(1-β)·g_t)
$$
参数 w1 自更新:w1.assign_sub(lr×m_w)
参数 b 自更新:b.assign_sub(lr×m_b)
(3)Adagrad,在 SGD 基础上增加二阶动量
$$
m_t=g_t
$$
$$
V_t=∑g_i^2
$$
$$
w_{t+1}=w_t-η_t=w_t-lr·g_t/(√V_t)
$$
(4)RMSProp,在 SGD 基础上增加二阶动量
$$
m_t=g_t
$$
$$
V_t=β·V_{t-1}+(1-β)·g_t^2
$$
$$
w_{t+1}=w_t-η_t=w_t-lr·g_t/(√V_t)
$$
(5)Adam,同时结合 SGDM 一阶动量和 RMSProp 二阶动量
$$
m_t=β1·m{t-1}+(1-β_1)·g_t
\ 修正一阶动量偏差:m_t’=\frac{m_t}{1-β_1^t}
$$
$$
V_t=β2·V{t-1}+(1-β_2)·g_t^2
\ 修正二阶动量的偏差:V_t’=\frac{V_t}{1-β_2^t}
$$
$$
w_{t+1}=w_t-η_t=w_t-lr·\frac{m_t}{1-β_1^t}/√(\frac{V_t}{1-β_2^t})
$$
2. 搭建神经网络
tensorflow 核心 API:tf.keras
2.1 六步法
import
train,test
a. 顺序网络结构:model=tf.keras.models.Sequential
b. 带跳连的非顺序结构:先定义网络类:calss MyModel(Model)
再调用 model=MyModel
model.compile
model.fit
model.summary
2.1.1 神经网络层
(1)顺序网络层
model=tf.keras.models.Sequential([网络结构]) #描述各层网络 网络结构有:
拉直层:tf.keras.layers.Flatten() ————> 不含计算,只是形状转换,把输入特征拉直为一维数组。
全连接层:
tf.keras.layers.Dense(神经元个数,activation=’激活函数’,kernel_regularizer= 哪种正则化)
卷积层:
tf.keras.layers.Dense(filters= 卷积核个数,kernel_size= 卷积核尺寸,strides= 卷积步长,padding=’valid’or’same’)
循环神经网络层 LSTM:
tf.keras.layers.LSTM()
(2)非顺序网络层
class MyModel(Model):
def __init__(self):
super(MyModel,self).__init__():
#这里定义网络结构快
def call(self,x):
#调用网络结构快,实现前向传播
return y
model=MyModel()2.1.2 神经网络配置
model.compile(optimizer= 优化器,loss= 损失函数,metrics=[' 准确率 '])(1)优化器
‘sgd’或者 tf.keras.optimizers.SGD(lr= 学习率,momentum= 动量参数)
‘adagrad’或者 tf.keras.optimizers.Adagred(lr= 学习率)
‘adadelta’或者 tf.keras.optimizers.Adadelta(lr= 学习率)
‘adam’或者 tf.keras.optimizers.Adam(lr= 学习率,beta_1=0.9,beta_2=0.999)
(2)损失函数 loss
‘mse’或者 tf.keras.losses.MeanSquaredError()
‘sparse_categorical_crossentropy’ 或者 tf.keras.losses.SparseCategoricalCrossentropy(from_logits=False)
神经网络经 softmax 函数概率分布输出,就设置 from_logits=False
不经过 softmax 函数概率分布输出概率输出,而是直接输出,则设置 from_logits=True
(3)准确率指标 Metrics
‘accuracy’:y_和 y 都是数值,如 y_=[1],y=[1]
‘categorical_accuracy’:y_和 y 都是独热码(概率分布),如 y_=[0,1,1],y=[0.256,0.695,0.048]
‘sparse_categorical_accuracy’:y_是数值,y 是独热码(概率分布),如 y_=[1],y=[0.256,0.695,0.048]
2.1.3 执行训练过程
model.fit(训练集的输入特征,训练集的标签,
batch_size=,epochs=,
validation_data=(测试集的输入特征,测试集的标签),
validation_split= 从训练集划分多少比例给测试集,
validation_freq= 多少次 epoch 测试一次)2.2 鸢尾花分类示例
(1)Sequential 搭建神经网络
import tensorflow as tf
from sklearn import datasets
import numpy as np
x_train=datasets.load_iris().data
y_lable=datasets.load_iris().target
np.random.seed(10)
np.random.shuffle(x_train)
np.random.seed(10)
np.random.shuffle(y_lable)
tf.random.set_seed(10)
# print(x_train,x_train.shape)
# print(y_lable)
model=tf.keras.models.Sequential([tf.keras.layers.Dense(4,activation='softmax',kernel_regularizer=tf.keras.regularizers.l2())
])
model.compile(optimizer=tf.keras.optimizers.SGD(lr=0.1),loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=False),
metrics=['sparse_categorical_accuracy'])
model.fit(x_train,y_lable,batch_size=32,epochs=50,validation_freq=20,validation_split=0.2)
model.summary()(2)class 类搭建神经网络
import tensorflow as tf
from sklearn import datasets
from tensorflow.keras.layers import Dense
from tensorflow.keras import Model
import numpy as np
x_train=datasets.load_iris().data
y_lable=datasets.load_iris().target
np.random.seed(10)
np.random.shuffle(x_train)
np.random.seed(10)
np.random.shuffle(y_lable)
tf.random.set_seed(10)
print(x_train,x_train.shape)
print(y_lable)
class IrisModel(Model):
def __init__(self):
super(IrisModel,self).__init__() #这里一定是要的
self.d1=Dense(4,activation='softmax',kernel_regularizer=tf.keras.regularizers.l2())
def call(self,x):
y=self.d1(x)
return y
model=IrisModel()
model.compile(optimizer=tf.keras.optimizers.SGD(lr=0.1),loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=False),
metrics=['sparse_categorical_accuracy'])
model.fit(x_train,y_lable,batch_size=32,epochs=50,validation_freq=20,validation_split=0.2)
model.summary()
2.3 mnist 数据集
提供 6 万张 28×28 像素点的 1-9 手写数字图片和标签,用于训练;
提供 1 万张 28×28 像素点的 1-9 手写数字图片和标签,用于测试;
数据集的导入:
mnist=tf.keras.datasets.mnist
(x_train,y_train),(x_test,y_test)=mnist.load.load_data()
作为输入特征,输入神经网络时,将数据拉伸为一维数组:
tf.keras.layers.Flatten()
Sequential 搭建神经网络代码如下:
import tensorflow as tf
import matplotlib.pyplot as plt
(x_train,y_train),(x_test,y_test)=tf.keras.datasets.mnist.load_data()
x_train,x_test=x_train/255,x_test/255
#print(y_train)
model=tf.keras.models.Sequential([tf.keras.layers.Flatten(),
tf.keras.layers.Dense(128,activation='relu'),
tf.keras.layers.Dense(10,activation='softmax'),
])
model.compile(optimizer='adam',loss='sparse_categorical_crossentropy',
metrics=['sparse_categorical_accuracy'])
history=model.fit(x_train,y_train,batch_size=32,epochs=8,validation_data=(x_test,y_test),
validation_freq=2)
model.summary()
// 输出结果如下:
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
flatten (Flatten) multiple 0
_________________________________________________________________
dense (Dense) multiple 100480
_________________________________________________________________
dense_1 (Dense) multiple 1290
=================================================================
Total params: 101,770
Trainable params: 101,770
Non-trainable params: 0
_________________________________________________________________
class 类搭建神经网络:
import tensorflow as tf
import matplotlib.pyplot as plt
from tensorflow.keras import Model
from tensorflow.keras.layers import Flatten,Dense
(x_train,y_train),(x_test,y_test)=tf.keras.datasets.mnist.load_data()
x_train,x_test=x_train/255,x_test/255
#print(y_train)
class MnistModel(Model):
def __init__(self):
super(MnistModel,self).__init__()
self.flatten=Flatten()
self.d1=Dense(128,activation='relu')
self.d2=Dense(10,activation='softmax')
def call(self,x):
x=self.flatten(x)
x=self.d1(x)
y=self.d2(x)
return y
model=MnistModel()
model.compile(optimizer='adam',loss='sparse_categorical_crossentropy',
metrics=['sparse_categorical_accuracy'])
history=model.fit(x_train,y_train,batch_size=32,epochs=8,validation_data=(x_test,y_test),
validation_freq=2)
model.summary()
// 输出结果如下:
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
flatten (Flatten) multiple 0
_________________________________________________________________
dense (Dense) multiple 100480
_________________________________________________________________
dense_1 (Dense) multiple 1290
=================================================================
Total params: 101,770
Trainable params: 101,770
Non-trainable params: 0
_________________________________________________________________
2.4 Fashion 数据集
提供 6 万张 28×18 像素点的衣服等图片和标签,用于训练。
提供 1 万张 28×18 像素点的衣服等图片和标签,用于测试。
Sequential 搭建神经网络代码如下:
import tensorflow as tf
import matplotlib.pyplot as plt
(x_train,y_train),(x_test,y_test)=tf.keras.datasets.fashion_mnist.load_data()
x_train,x_test=x_train/255,x_test/255
#剩下代码同 minist 数据集代码3. 黑白图片应用
以上的示例都是自带准备好的数据集,直接可以拿来用,如果是我们自己的训练数据包,该如何处理成为规范化成为可以喂入神经网络的数据呢?
这里提出两个概念:自制数据集和数据增强!
数据增强:是针对于你的数据量过少,模型训练不足,泛化力会弱,这时就需要数据增强。
还有一个问题是,我们已有一些数据集,已经训练好了参数,但后面又需补充一些新的数据,如果这时又重新加入新数据重头再训练,就显得太笨了,
这时就需要 断点续训 了!实时保存最优模型。
训练神经网络的目的就是要获取各层神经网络的最优参数,只要拿到这些参数,就能跨机跨平台使用了,这时就需要 参数提取 了。
与此同时,我们还需要见证模型的优化过程,到底是不是在往好的方向优化,这时就需要绘制 acc/loss 曲线 了!
最后,训练出模型,我们就需要用它干点事了,给神经网络一组新的数据,实现前向推理,让神经网络 预测 出结果,实现学以致用!
以上归纳就是如下:
①自制数据集,解决本领域的应用
②数据增强,扩充数据集
③断点续训,存取模型
④参数提取,把参数存入文本
⑤acc/loss 可视化,查看训练结果
⑥应用程序,给物识图
3.1 自制数据集
准备两个文件夹:
trian_jpg_60000 用于放置训练的图片
test_jpg_10000 用于放置测试的图片
准备两个 txt 文件:
train_label_60000.txt 用于放置训练的图片名及其对应标签
test_label_10000.txt 用于放置测试的图片名及其对应标签
txt 文本文件内容示例如下:

实现代码如下:
from PIL import Image
import numpy as np
import os
def generated(path,txt): #将原生图片转换成数组格式
f=open(txt,'r')
contents=f.readlines()
f.close()
x,y=[],[]
for content in contents:
img_name=content.split()[0]
img_label=content.split()[1]
img_path=path+'\\'+img_name
img=Image.open(img_path)
img=np.array(img.convert('L'))
img=img/255.
x.append(img)
y.append(img_label)
print('loading:',img_name)
x=np.array(x)
y=np.array(y)
y=y.astype(np.int64)
return x,y
train_img_path='D:\\ 北大 tf2 课程 \\ 制作数据集 \\mnist_train_jpg_60000' #训练图片文件夹, 这里是 6000 张 28×28 像素的图片
train_label_path='D:\\ 北大 tf2 课程 \\ 制作数据集 \\mnist_train_jpg_60000.txt' #训练图片对应的 txt 文件
test_img_path='D:\\ 北大 tf2 课程 \\ 制作数据集 \\mnist_test_jpg_10000' #测试图片文件夹
test_label_path='D:\\ 北大 tf2 课程 \\ 制作数据集 \\mnist_test_jpg_10000.txt' #测试图片对应的 txt 文件
train_datasets_path='D:\\ 北大 tf2 课程 \\ 制作数据集 \\mnist_train.npy' #训练图片转换成可用数据集,这里设置其存储路径及格式
train_label_datasets_path='D:\\ 北大 tf2 课程 \\ 制作数据集 \\mnist_train_label.npy' #训练图片标签转换成可用数据集,这里设置其存储路径及格式
test_datasets_path='D:\\ 北大 tf2 课程 \\ 制作数据集 \\mnist_test.npy' #测试图片转换成可用数据集,这里设置其存储路径及格式
test_label_datasets_path='D:\\ 北大 tf2 课程 \\ 制作数据集 \\mnist_test_label.npy' #测试图片标签转换成可用数据集,这里设置其存储路径及格式
if not os.path.exists(train_datasets_path) and not os.path.exists(train_label_datasets_path) and not os.path.exists(test_datasets_path) and not os.path.exists(test_label_datasets_path):
print('-------------Generate Datasets-----------------')
x_train, y_lable = generated(train_img_path, train_label_path)
x_test, y_test_label = generated(test_img_path, test_label_path)
print('-------------Save Datasets-----------------')
x_train = np.reshape(x_train, (len(x_train), -1))
x_test = np.reshape(x_test, (len(x_test), -1))
np.save(train_datasets_path,x_train)
np.save(train_label_datasets_path,y_lable)
np.save(test_datasets_path,x_test)
np.save(test_label_datasets_path,y_test_label)
else:
print('-------------Load Datasets-----------------')
x_train = np.load(train_datasets_path)
y_label = np.load(train_label_datasets_path)
x_test = np.load(test_datasets_path)
y_test_label = np.load(test_label_datasets_path)
x_train = np.reshape(x_train, (len(x_train), 28, 28))
x_test = np.reshape(x_test, (len(x_test), 28, 28))
print(x_train.shape,y_label.shape)
print(x_test,y_test_label)3.2 数据增强
image_gen_train=tf.keras.preprocessing.image.ImageDataGenerator(增强方法)
image_gen_train.fit(x_train)
常用增强方法:
缩放系数:rescale= 所有数据将乘以该系数
随机旋转:rotation_range= 随机旋转角度范围
宽度偏移:width_shift_range= 随机宽度偏移量
高度偏移:height_shift_range= 随机高度偏移量
水平旋转:horizontal_flip= 是否水平随机翻转
随机缩放:zoom_range= 随机缩放的范围 [1-n,1+n]

model.fit(……)更新为:
model.fit(image_gen_train.flow(x_train,y_train,batch_size=),...)
代码示例:
import tensorflow as tf
from tensorflow.keras.preprocessing.image import ImageDataGenerator
mnist = tf.keras.datasets.mnist
(x_train, y_train), (x_test, y_test) = mnist.load_data()
x_train, x_test = x_train / 255.0, x_test / 255.0
x_train = x_train.reshape(x_train.shape[0], 28, 28, 1) # 给数据增加一个维度, 从(60000, 28, 28)reshape 为(60000, 28, 28, 1)
image_gen_train = ImageDataGenerator(
rescale=1. / 1., # 如为图像,分母为 255 时,可归至 0~1
rotation_range=45, # 随机 45 度旋转
width_shift_range=.15, # 宽度偏移
height_shift_range=.15, # 高度偏移
horizontal_flip=False, # 水平翻转
zoom_range=0.5 # 将图像随机缩放阈量 50%
)
image_gen_train.fit(x_train)
model = tf.keras.models.Sequential([tf.keras.layers.Flatten(),
tf.keras.layers.Dense(128, activation='relu'),
tf.keras.layers.Dense(10, activation='softmax')
])
model.compile(optimizer='adam', loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=False),
metrics=['sparse_categorical_accuracy'])
model.fit(image_gen_train.flow(x_train, y_train, batch_size=32), epochs=5, validation_data=(x_test, y_test),
validation_freq=1)
model.summary()3.3 保存及读取模型
保存模型:
cp_callback=tf.keras.callbacks.ModelCheckpoint(
filepath=' 路径文件名 ',
save_weights_only=True/False,
save_best_only=True/False)
model.fit(...,callback=[cp_callback])读取模型:
model.load_weights(' 路径文件名 ')应用示例如下:
import tensorflow as tf
import os
mnist = tf.keras.datasets.mnist
(x_train, y_train), (x_test, y_test) = mnist.load_data()
x_train, x_test = x_train / 255.0, x_test / 255.0
model = tf.keras.models.Sequential([tf.keras.layers.Flatten(),
tf.keras.layers.Dense(128, activation='relu'),
tf.keras.layers.Dense(10, activation='softmax')
])
model.compile(optimizer='adam',
loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=False),
metrics=['sparse_categorical_accuracy'])
checkpoint_save_path = "./checkpoint/mnist.ckpt"
if os.path.exists(checkpoint_save_path + '.index'):
print('-------------load the model-----------------')
model.load_weights(checkpoint_save_path)
cp_callback = tf.keras.callbacks.ModelCheckpoint(filepath=checkpoint_save_path,
save_weights_only=True,
save_best_only=True)
history = model.fit(x_train, y_train, batch_size=32, epochs=5,
validation_data=(x_test, y_test), validation_freq=1,
callbacks=[cp_callback])
#调用 callbacks 后会在加载模型基础上继续训练
model.summary()3.4 参数提取
提取可训练参数:
model.trainable_variables 返回模型中可训练参数
设置 print 输出格式
np.set_printoptions(threshold= 超过多少省略显示) #np.inf 表示无限大
model.sumary() #sumary 之后可接上以下代码实现参数提取
print(model.trainable_variables)
file=open('./weights.txt','w')
for v in model.trainable_variables:
file.write(str(v.name)+'\n')
file.write(str(v.shape)+'\n')
file.write(str(v.numpy())+'\n')
file.close()3.5 acc/loss 可视化
history=model.fit(...)
acc=history.history['sparse_categorical_accuracy'] #训练集准确率
val_acc=history.history['val_sparse_categorical_accuracy'] #测试集准确率
loss=history.history['loss'] #训练集损失率
val_loss=history.history['val_loss'] #测试集损失率
plt.subplot(1,2,1)
plt.plot(acc,label='Training Accuracy')
plt.plot(val_acc,label='Validation Accuracy')
plt.title('training and validation accuracy')
plt.legend()
plt.subplot(1,2,2)
plt.plot(loss,label='Training loss')
plt.plot(val_loss,label='Validation loss')
plt.title('training and validation loss')
plt.legend()
plt.show()3.6 给图识物
model=tf.keras.models.Sequentical([tf.keras.layers.Flatten(),
tf.keras.layers.Dense(128,activation='relu'),
tf.keras.layers.Dense(10,activation='softmax'),
])
model.load_weights(model_save_path)
result=model.predict(x_predict)应用示例:
from PIL import Image
import numpy as np
import tensorflow as tf
model_save_path = './checkpoint/mnist.ckpt'
model = tf.keras.models.Sequential([tf.keras.layers.Flatten(),
tf.keras.layers.Dense(128, activation='relu'),
tf.keras.layers.Dense(10, activation='softmax')])
model.load_weights(model_save_path)
preNum = int(input("input the number of test pictures:"))
for i in range(preNum):
image_path = input("the path of test picture:")
img = Image.open(image_path)
img = img.resize((28, 28), Image.ANTIALIAS) #以高质量缩放到 28×28size 大小
img_arr = np.array(img.convert('L'))
for i in range(28):
for j in range(28):
if img_arr[i][j] < 200:
img_arr[i][j] = 255
else:
img_arr[i][j] = 0
img_arr = img_arr / 255.0
x_predict = img_arr[tf.newaxis, ...] #这行代码很重要!将(28,28)变成(1,28,28)
result = model.predict(x_predict)
pred = tf.argmax(result, axis=1)
print('\n')
tf.print(pred)补充点:
Image.NEAREST :低质量
Image.BILINEAR:双线性
Image.BICUBIC :三次样条插值
Image.ANTIALIAS:高质量
4. 彩色图片应用
现实世界中,实际项目中的图片多是高分辨率彩色图,包含 RGB 三通道。
图片色彩丰富会导致待优化的参数过多,容易造成模型过拟合。
实际应用时会把原始图片进行特征提取,再把提取到的特征送给全连接网络。
4.1 卷积神经网络
卷积计算是一种有效的提取图像特征的方法。
一般会采用一个正方形的卷积核,按指定步长,在输入特征图上滑动,遍历输入特征图中每个像素点。每一个步长,卷积核会与输入特征图出现重合区域,重合区域对应元素相乘,求和再加上偏置项,得到输入特征的一个像素点。
输入特征图的深度,决定了当前层卷积核的深度。如黑白为一维,RGB 彩色图为三维。
当前卷积核的个数,决定了当前层输出特征图的深度。
卷积计算过程:
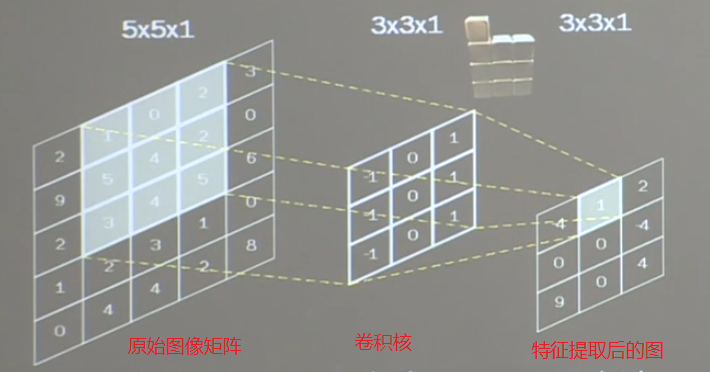
原始图像矩阵与卷积核对应位置的像素点值进行乘运算,最后把这九个值相加,并加上偏置项 1。
1×(-1)+0×0+2×1+5×(-1)+4×0+2×1+3×(-1)+4×0+5×1+1=1
以上可以看到,5×5 的图片经过 3×3 卷积核计算,输出图片变成了 3×3,大大减少了图片信息量,有利于模型训练。
感受野
Receptive Field,卷积神经网络各输入特征图中的每个像素点,在原始输入图片上映射区域的大小。
全零填充

在原始图像像素矩阵四周加 0,使得在卷积计算过程中,输出结果图片大小与原图片一致。

以上公式表现了是否采用全零填充时,原图片与输出图片,步长,核长四者之间的关系。
TF 描述卷积层:
tf.keras.layers.Conv2D(
filters= 卷积核个数,
kernel_size= 卷积核尺寸, #也可 (高,宽) 给出
strides= 滑动步长, # 默认 1
padding='same'or'valid, #全零填充是 'same', 默认 'valid'
activation=' 激活函数 ', #若有 BN 此处不写
input_shape=(高,宽,通道数), #输入特征维度,可省略
)4.1.2 批标准化 BN
输入数据经过网络训练之后,由于权重的不同,可能造成输出数据变得过大或过小,这样进行激活时,如使用 tanh 函数激活,一旦 x 值超过 2 之后,其激活效果没有差别,激活函数对 0 附近的数据更加敏感。
神经网络对 0 附近的数据更敏感,但是随着网络层数的增加,特征数据会出现偏离 0 均值的情况,这时可以通过标准化进行调整。
标准化:使数据整体符合 0 均值,1 为标准差的分布。
批标准化:对一小批数据,做标准化处理
为每个卷积核引入可训练参数γi,βi,调整批归一化的力度。使得输出数据过激活函数前,进行统一的标准化处理。
不用担心批标准化之后改变原数据之间的关系,本来有的特征就是需要强化,有的需要弱化,所有的这些可训练参数(权重 w,偏置项 b,标准化参数γi,βi等)经过训练之后,通过固定的相配对的网络结构就能准确反映预期的结果。
目的:提升激活函数对输入数据的区分力。
BN 层位于卷积层之后,激活层之前。
TF 描述批标准化
tf.keras.layers.BatchNormalization()
model=tf.keras.models.Sequential([Conv2D(filters=6,kernel_size=(5,5),padding='same'),
BatchNormalization(),
Activation('relu'),
MaxPool2D(pool_size=(2,2),strides=2,padding='same'),
Dropout(0.2)
])4.1.3 池化
目的:减少特征数据量
所谓池化,就是取目标图片像素矩阵中一块区域数值的最大值,或均值来代替原图片像素矩阵。
最大值池化可提取图片纹理,均值池化可保留背景特征。

TF 描述池化
tf.keras.layers.MaxPool2D(
pool_size= 池化核尺寸,
strides= 滑动步长, # 默认 pool_size
padding='same'or'valid, #全零填充是 'same', 默认 'valid'
)
tf.keras.layers.AveragePooling2D(
pool_size= 池化核尺寸,
strides= 滑动步长, # 默认 pool_size
padding='same'or'valid, #全零填充是 'same', 默认 'valid'
)
4.1.4 舍弃
为了缓解神经网络过拟合,在神经网络训练中,将隐藏层一部分神经元按照一定概率从神经网络中暂时舍弃。神经网络使用时,被舍弃的神经元恢复连接。
TF 描述池化:
tf.keras.layers.Dropout(舍弃概率)
4.1.5 总结
卷积神经网络:借助卷积核提取特征后,送入全连接网络。
卷积神经网络主要模块:


4.2 应用
以 Cifar10 数据集为例:
提供 5 万张 32×32 像素点的十分类彩色图片和标签,用于训练。
提供 1 万张 32×32 像素点的十分类彩色图片和标签,用于测试。
一共有十类动物图片。
导入 cifar10 数据集:
cifar10=tf.keras.datasets.cifar10
(x_train,y_train),(x_test,y_test)=cifar10.load_data()实现示例:
import tensorflow as tf
import os
import matplotlib.pyplot as plt
from tensorflow.keras.models import Model
from tensorflow.keras.layers import Conv2D,BatchNormalization,Activation,MaxPool2D,Dropout,Flatten,Dense
cifar10=tf.keras.datasets.cifar10
(x_train,y_train),(x_test,y_test)=cifar10.load_data()
x_train=x_train/255.
x_test=x_test/255.
class Baseline(Model):
def __init__(self):
super(Baseline,self).__init__()
self.c1=Conv2D(filters=6,kernel_size=5,padding='same')
self.b1=BatchNormalization()
self.a1=Activation('relu')
self.p1=MaxPool2D(pool_size=2,strides=2,padding='same')
self.d1=Dropout(0.2)
self.f1=Flatten()
self.d2=Dense(128,activation='relu')
self.d3=Dropout(0.2)
self.d4=Dense(10,activation='softmax')
def call(self,x):
x=self.c1(x)
x=self.b1(x)
x=self.a1(x)
x=self.p1(x)
x=self.d1(x)
x=self.f1(x)
x=self.d2(x)
x=self.d3(x)
y=self.d4(x)
return y
model=Baseline()
model.compile(optimizer=tf.keras.optimizers.Adam(lr=0.1),
loss='sparse_categorical_crossentropy',
metrics=['sparse_categorical_accuracy'])
model_path='./checkpoint/cifar10.ckpt'
if os.path.exists(model_path+'.index'):
print('loading model')
model.load_weights(model_path)
cp_callback=tf.keras.callbacks.ModelCheckpoint(filepath=model_path,
save_best_only=True,
save_weights_only=True)
history=model.fit(x_train,y_train,batch_size=32,epochs=9,
validation_data=(x_test,y_test),
validation_freq=1,callbacks=[cp_callback])
model.summary()
loss=history.history['loss']
val_loss=history.history['val_loss']
acc=history.history['sparse_categorical_accuracy']
val_acc=history.history['val_sparse_categorical_accuracy']
plt.subplot(121)
plt.plot(loss,label='loss')
plt.plot(val_loss,label='val_loss')
plt.legend()
plt.subplot(122)
plt.plot(acc,label='acc')
plt.plot(val_acc,label='val_acc')
plt.legend()
plt.show()5. 经典卷积神经网络

5.1 LeNet

LeNet 神经网络结果如上,运用了:
两个卷积神经网络 + 一个拉直层 + 三个全连接网络
5.2 AlexNet
AlexNet 网络诞生于 2012 年,当年的 ImageNet 竞赛的冠军,Top5 错误率为 16.4%。
Alex Krizhevsky, Ilya Sutskever; Geoffrey E. Hinton. ImageNet Classfication with Deep Convolution Networks. In NIPS 2012.
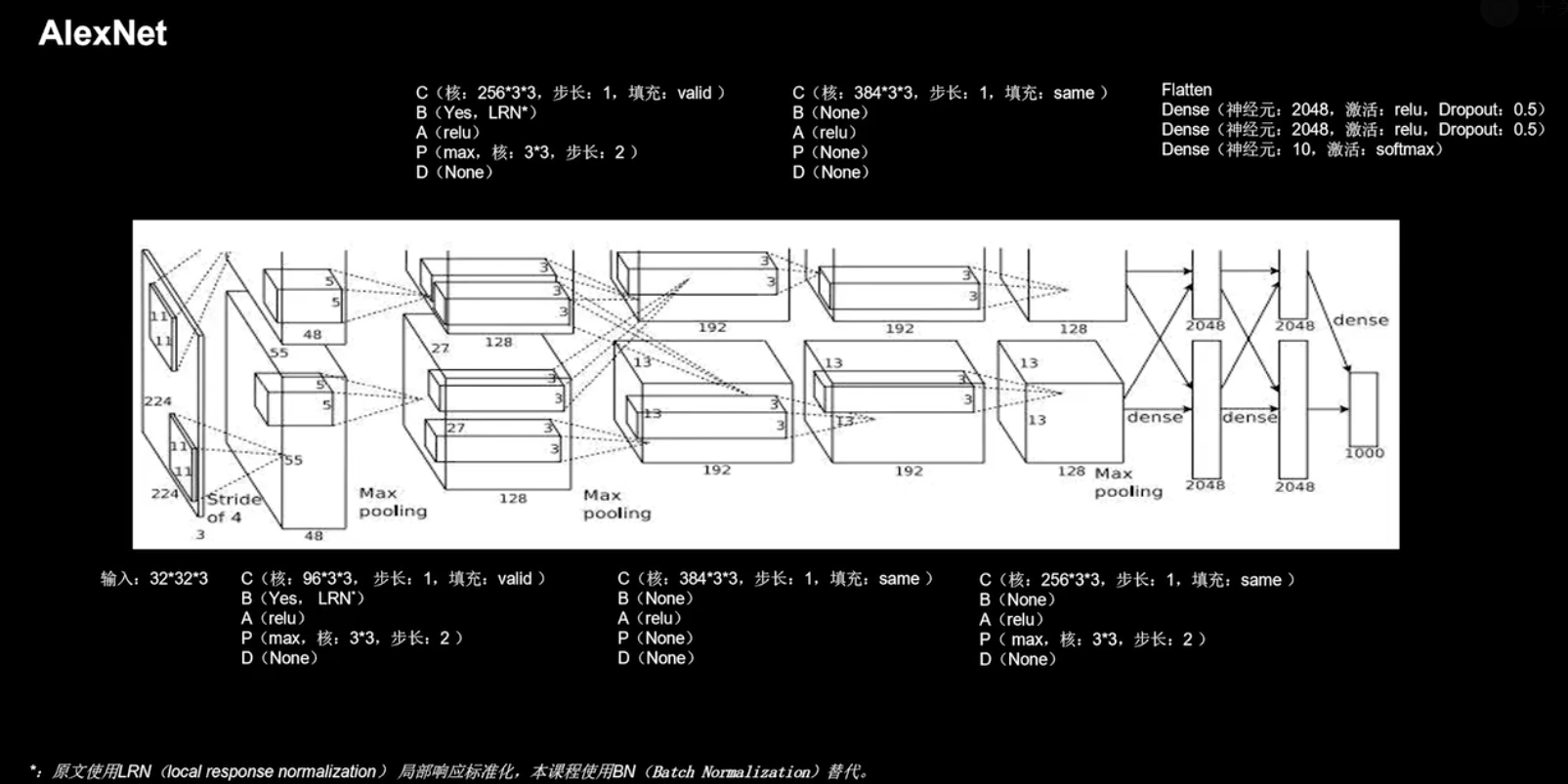
AlexNet 神经网络结果如上,运用了:
五个卷积神经网络 + 一个拉直层 + 三个全连接网络
5.3 VGGNet
VGGNet 诞生于 2014 年,当年 ImageNet 竞赛的亚军,Top5 错误率减小到 7.3%。使用小尺寸卷积核,减少了参数的同时提高了准确率,其网络结构规整,非常适合硬件加速。
K Simonyan, A Zisserman. Very Deep Convolutional Networks for Large Scale Image RecognitionI. In NIPS 2015.
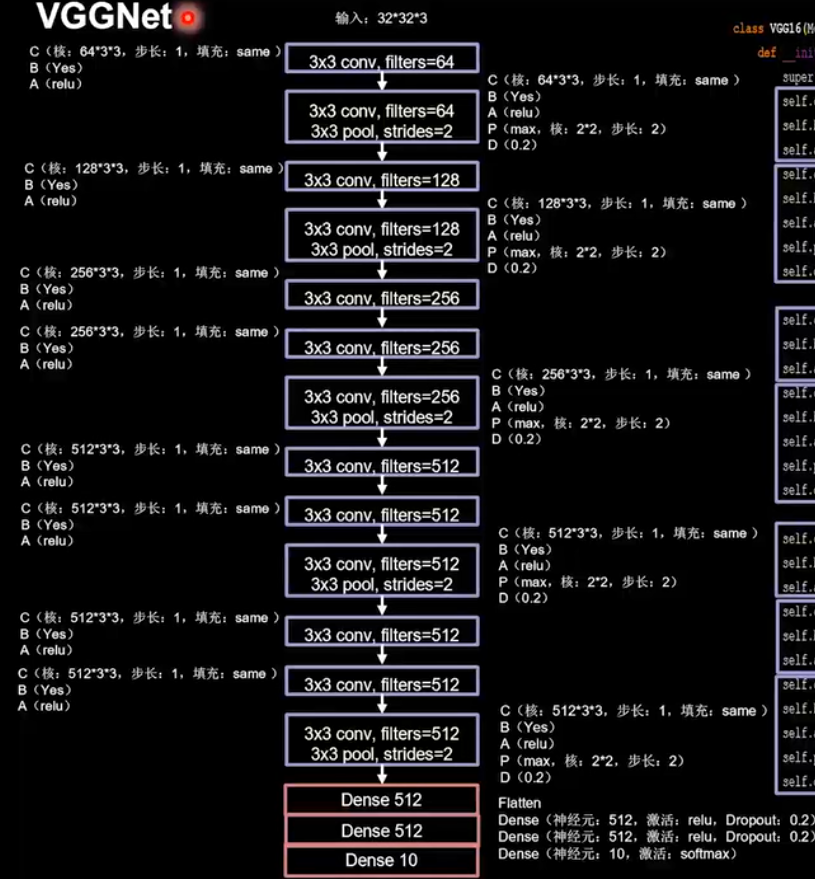
VGGNet 神经网络结果如上,运用了:
十三个卷积神经网络 + 一个拉直层 + 三个全连接网络
5.4 InceptionNet
InceptionNet 诞生于 2014 年,当年 ImageNet 竞赛的亚军,Top5 错误率减小到 6.67%。
SzegedyC, Liu w, Jia y, et al. Going Deeper with Convolutions. In CVPR, 2015.
引入 Inception 结构块,在同一层网络内使用不同尺寸的卷积核,提升了模型感知力,使用批标准化,缓解了梯度消失。
InceptionNet 的核心是它的基本单元 Inception 结构块,包括其后续版本,都是基于 Inception 结构块搭建的网络。
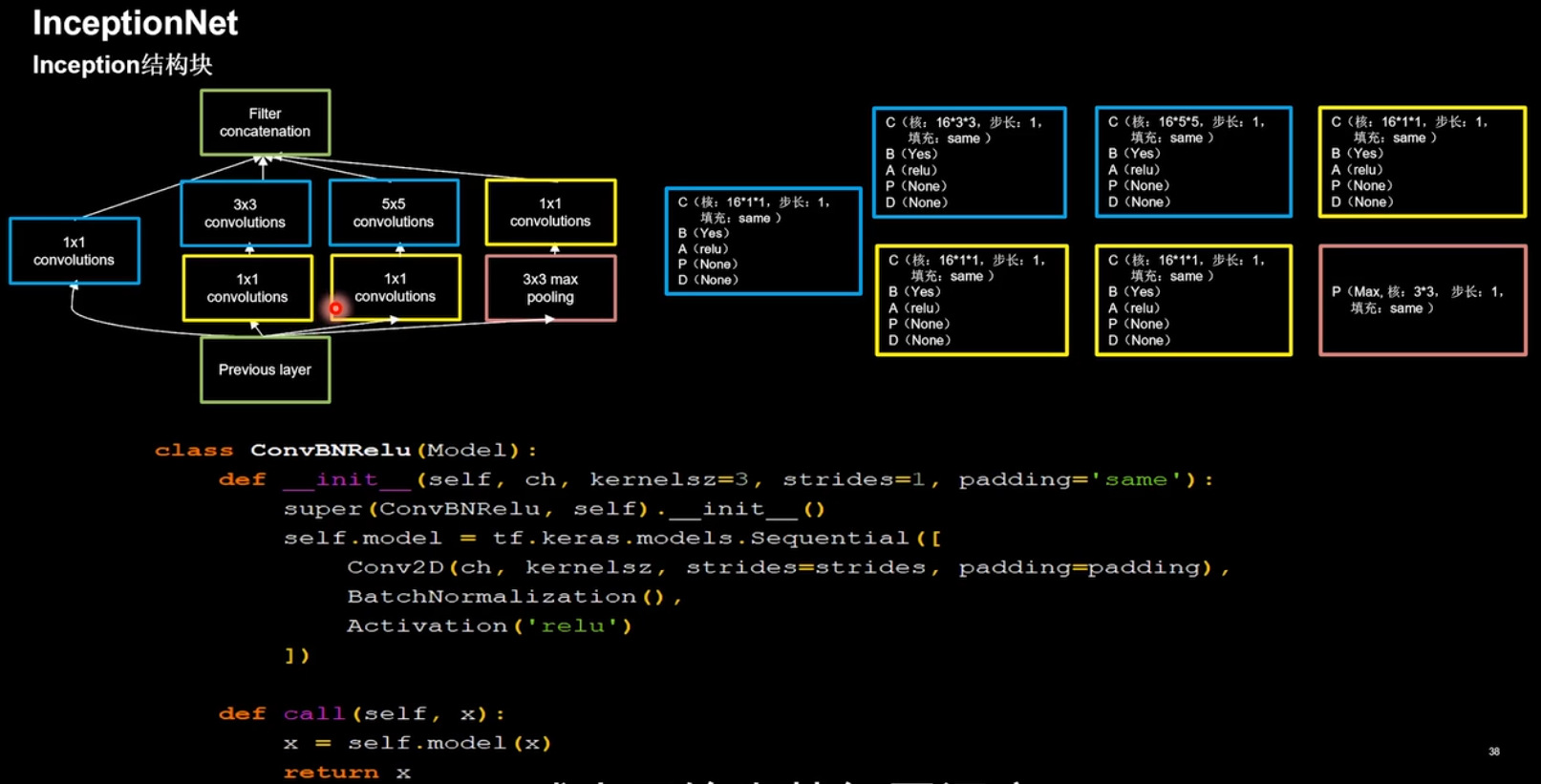
实现代码如下:
import tensorflow as tf
import os
import numpy as np
from matplotlib import pyplot as plt
from tensorflow.keras.layers import Conv2D, BatchNormalization, Activation, MaxPool2D, Dropout, Flatten, Dense, GlobalAveragePooling2D
from tensorflow.keras import Model
np.set_printoptions(threshold=np.inf) #设置输出打印格式
cifar10 = tf.keras.datasets.cifar10
(x_train, y_train), (x_test, y_test) = cifar10.load_data()
x_train, x_test = x_train / 255.0, x_test / 255.0
class ConvBNRelu(Model):
def __init__(self, ch, kernelsz=3, strides=1, padding='same'):
super(ConvBNRelu, self).__init__()
self.model = tf.keras.models.Sequential([Conv2D(ch, kernelsz, strides=strides, padding=padding),
BatchNormalization(),
Activation('relu')
])
def call(self, x):
x = self.model(x, training=False)
#在 training=False 时,BN 通过整个训练集计算均值、方差去做批归一化,training=True 时,通过当前 batch 的均值、方差去做批归一化。推理时 training=False 效果好
return x
class InceptionBlk(Model):
def __init__(self, ch, strides=1):
super(InceptionBlk, self).__init__()
self.ch = ch
self.strides = strides
self.c1 = ConvBNRelu(ch, kernelsz=1, strides=strides)
self.c2_1 = ConvBNRelu(ch, kernelsz=1, strides=strides)
self.c2_2 = ConvBNRelu(ch, kernelsz=3, strides=1)
self.c3_1 = ConvBNRelu(ch, kernelsz=1, strides=strides)
self.c3_2 = ConvBNRelu(ch, kernelsz=5, strides=1)
self.p4_1 = MaxPool2D(3, strides=1, padding='same')
self.c4_2 = ConvBNRelu(ch, kernelsz=1, strides=strides)
def call(self, x):
x1 = self.c1(x)
x2_1 = self.c2_1(x)
x2_2 = self.c2_2(x2_1)
x3_1 = self.c3_1(x)
x3_2 = self.c3_2(x3_1)
x4_1 = self.p4_1(x)
x4_2 = self.c4_2(x4_1)
# concat along axis=channel
x = tf.concat([x1, x2_2, x3_2, x4_2], axis=3)
return x
class Inception10(Model):
def __init__(self, num_blocks, num_classes, init_ch=16, **kwargs):
super(Inception10, self).__init__(**kwargs)
self.in_channels = init_ch
self.out_channels = init_ch
self.num_blocks = num_blocks
self.init_ch = init_ch
self.c1 = ConvBNRelu(init_ch)
self.blocks = tf.keras.models.Sequential()
for block_id in range(num_blocks):
for layer_id in range(2):
if layer_id == 0:
block = InceptionBlk(self.out_channels, strides=2)
else:
block = InceptionBlk(self.out_channels, strides=1)
self.blocks.add(block)
# enlarger out_channels per block
self.out_channels *= 2
self.p1 = GlobalAveragePooling2D()
self.f1 = Dense(num_classes, activation='softmax')
def call(self, x):
x = self.c1(x)
x = self.blocks(x)
x = self.p1(x)
y = self.f1(x)
return y
model = Inception10(num_blocks=2, num_classes=10)
model.compile(optimizer='adam',
loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=False),
metrics=['sparse_categorical_accuracy'])
checkpoint_save_path = "./checkpoint/Inception10.ckpt"
if os.path.exists(checkpoint_save_path + '.index'):
print('-------------load the model-----------------')
model.load_weights(checkpoint_save_path)
cp_callback = tf.keras.callbacks.ModelCheckpoint(filepath=checkpoint_save_path,
save_weights_only=True,
save_best_only=True)
history = model.fit(x_train, y_train, batch_size=32,
epochs=5, validation_data=(x_test, y_test),
validation_freq=1,
callbacks=[cp_callback])
model.summary()5.5 ResNet
ResNet 诞生于 2015 年,当年 ImageNet 竞赛冠军,Top5 错误率为 3.57%。
Kaiming He, Xiangyu Zhang, Shaoqing Ren. Deep Residual Learning for Image Recognition. InCPVR2016.
单纯叠加网络层数会使神经网络模型退化,以至于后面的特征丢失了前边特征的原本模样。
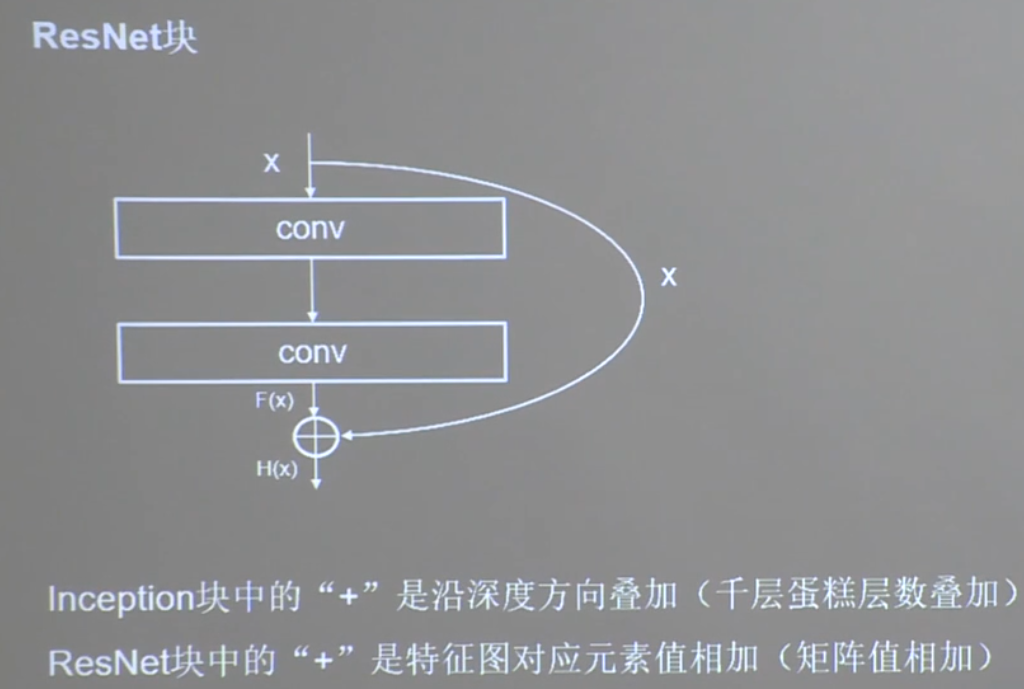
上述有效缓解了神经网络模型堆叠导致的退化,使得神经网络可以朝着更深层级的方向发展。

实现代码如下:
import tensorflow as tf
import os
import numpy as np
from matplotlib import pyplot as plt
from tensorflow.keras.layers import Conv2D, BatchNormalization, Activation, MaxPool2D, Dropout, Flatten, Dense
from tensorflow.keras import Model
np.set_printoptions(threshold=np.inf)
cifar10 = tf.keras.datasets.cifar10
(x_train, y_train), (x_test, y_test) = cifar10.load_data()
x_train, x_test = x_train / 255.0, x_test / 255.0
class ResnetBlock(Model):
def __init__(self, filters, strides=1, residual_path=False):
super(ResnetBlock, self).__init__()
self.filters = filters
self.strides = strides
self.residual_path = residual_path
self.c1 = Conv2D(filters, (3, 3), strides=strides,
padding='same', use_bias=False)
self.b1 = BatchNormalization()
self.a1 = Activation('relu')
self.c2 = Conv2D(filters, (3, 3), strides=1,
padding='same', use_bias=False)
self.b2 = BatchNormalization()
# residual_path 为 True 时,对输入进行下采样,即用 1x1 的卷积核做卷积操作,保证 x 能和 F(x)维度相同,顺利相加
if residual_path:
self.down_c1 = Conv2D(filters, (1, 1), strides=strides,
padding='same', use_bias=False)
self.down_b1 = BatchNormalization()
self.a2 = Activation('relu')
def call(self, inputs):
residual = inputs # residual 等于输入值本身,即 residual=x
# 将输入通过卷积、BN 层、激活层,计算 F(x)
x = self.c1(inputs)
x = self.b1(x)
x = self.a1(x)
x = self.c2(x)
y = self.b2(x)
if self.residual_path:
residual = self.down_c1(inputs)
residual = self.down_b1(residual)
out = self.a2(y + residual) # 最后输出的是两部分的和,即 F(x)+x 或 F(x)+Wx, 再过激活函数
return out
class ResNet18(Model):
def __init__(self, block_list, initial_filters=64): # block_list 表示每个 block 有几个卷积层
super(ResNet18, self).__init__()
self.num_blocks = len(block_list) # 共有几个 block
self.block_list = block_list
self.out_filters = initial_filters
self.c1 = Conv2D(self.out_filters, (3, 3), strides=1,
padding='same', use_bias=False)
self.b1 = BatchNormalization()
self.a1 = Activation('relu')
self.blocks = tf.keras.models.Sequential()
# 构建 ResNet 网络结构
for block_id in range(len(block_list)): # 第几个 resnet block
for layer_id in range(block_list[block_id]): # 第几个卷积层
if block_id != 0 and layer_id == 0: # 对除第一个 block 以外的每个 block 的输入进行下采样
block = ResnetBlock(self.out_filters, strides=2,
residual_path=True)
else:
block = ResnetBlock(self.out_filters, residual_path=False)
self.blocks.add(block) # 将构建好的 block 加入 resnet
self.out_filters *= 2 # 下一个 block 的卷积核数是上一个 block 的 2 倍
self.p1 = tf.keras.layers.GlobalAveragePooling2D()
self.f1 = tf.keras.layers.Dense(10, activation='softmax',
kernel_regularizer=tf.keras.regularizers.l2())
def call(self, inputs):
x = self.c1(inputs)
x = self.b1(x)
x = self.a1(x)
x = self.blocks(x)
x = self.p1(x)
y = self.f1(x)
return y
model = ResNet18([2, 2, 2, 2])
model.compile(optimizer='adam',
loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=False),
metrics=['sparse_categorical_accuracy'])
checkpoint_save_path = "./checkpoint/ResNet18.ckpt"
if os.path.exists(checkpoint_save_path + '.index'):
print('-------------load the model-----------------')
model.load_weights(checkpoint_save_path)
cp_callback = tf.keras.callbacks.ModelCheckpoint(filepath=checkpoint_save_path,
save_weights_only=True,
save_best_only=True)
history = model.fit(x_train, y_train, batch_size=32, epochs=5,
validation_data=(x_test, y_test), validation_freq=1,
callbacks=[cp_callback])
model.summary()5.6 小结

6. 循环神经网络 RNN
实现连续数据的预测,根据上文,预测下文:如输入 abc,系统可以预测下一步是 d;如输入鱼离不开__,系统能预测空格应该填入水。
6.1 循环核
循环核:参数时间共享,循环层提取时间信息。
循环核具有记忆力,通过不同时刻的参数共享,实现了对时间序列的信息提取。

前向传播时,记忆体内存储的状态信息 ht,在每个时刻都被刷新,三个参数矩阵 wxh,whh,why自始至终都是固定不变的。
反向传播时,三个参数矩阵 wxh,whh,why被梯度下降法更新。
yt=softmax(htwhy+by)
ht=tanh(xtwxh+ht-1whh+bh)
循环神经网络:借助循环核提取时间特征后,送入全连接网络。
6.2 TF 描述循环记忆层
tf.keras.layers.SimpleRNN(记忆体个数,activation=' 激活函数 ',
return_sequences= 是否每个时刻输出 ht 到下一层)activation=’激活函数’,默认使用 tanh。
return_sequences=True,各时间步输出 ht
return_sequences=False,仅最后时间步输出 ht(默认)
入 RNN 时,x_train 维度:
[送入样本数,循环核时间展开步数,每个时间步输入特征个数]
如下图:

若输入 4 个字母出结果,循环核时间展开步数为 4。
6.3 应用
6.3.1 依次预
import numpy as np
import tensorflow as tf
from tensorflow.keras.layers import Dense, SimpleRNN
import matplotlib.pyplot as plt
import os
input_word = "abcde"
w_to_id = {'a': 0, 'b': 1, 'c': 2, 'd': 3, 'e': 4} # 单词映射到数值 id 的词典
id_to_onehot = {0: [1., 0., 0., 0., 0.], 1: [0., 1., 0., 0., 0.], 2: [0., 0., 1., 0., 0.], 3: [0., 0., 0., 1., 0.],
4: [0., 0., 0., 0., 1.]} # id 编码为 one-hot
x_train = [id_to_onehot[w_to_id['a']], id_to_onehot[w_to_id['b']], id_to_onehot[w_to_id['c']],
id_to_onehot[w_to_id['d']], id_to_onehot[w_to_id['e']]]
y_train = [w_to_id['b'], w_to_id['c'], w_to_id['d'], w_to_id['e'], w_to_id['a']]
np.random.seed(7)
np.random.shuffle(x_train)
np.random.seed(7)
np.random.shuffle(y_train)
tf.random.set_seed(7)
# 使 x_train 符合 SimpleRNN 输入要求:[送入样本数, 循环核时间展开步数, 每个时间步输入特征个数]。
# 此处整个数据集送入,送入样本数为 len(x_train);输入 1 个字母出结果,循环核时间展开步数为 1; 表示为独热码有 5 个输入特征,每个时间步输入特征个数为 5
x_train = np.reshape(x_train, (len(x_train), 1, 5))
y_train = np.array(y_train)
model = tf.keras.Sequential([SimpleRNN(3),
Dense(5, activation='softmax')
])
#以下省略6.3.2 连续预测
import numpy as np
import tensorflow as tf
from tensorflow.keras.layers import Dense, SimpleRNN
import matplotlib.pyplot as plt
import os
input_word = "abcde"
w_to_id = {'a': 0, 'b': 1, 'c': 2, 'd': 3, 'e': 4} # 单词映射到数值 id 的词典
id_to_onehot = {0: [1., 0., 0., 0., 0.], 1: [0., 1., 0., 0., 0.],
2: [0., 0., 1., 0., 0.], 3: [0., 0., 0., 1., 0.],
4: [0., 0., 0., 0., 1.]} # id 编码为 one-hot
x_train = [[id_to_onehot[w_to_id['a']], id_to_onehot[w_to_id['b']], id_to_onehot[w_to_id['c']], id_to_onehot[w_to_id['d']]],
[id_to_onehot[w_to_id['b']], id_to_onehot[w_to_id['c']], id_to_onehot[w_to_id['d']], id_to_onehot[w_to_id['e']]],
[id_to_onehot[w_to_id['c']], id_to_onehot[w_to_id['d']], id_to_onehot[w_to_id['e']], id_to_onehot[w_to_id['a']]],
[id_to_onehot[w_to_id['d']], id_to_onehot[w_to_id['e']], id_to_onehot[w_to_id['a']], id_to_onehot[w_to_id['b']]],
[id_to_onehot[w_to_id['e']], id_to_onehot[w_to_id['a']], id_to_onehot[w_to_id['b']], id_to_onehot[w_to_id['c']]],
]
y_train = [w_to_id['e'], w_to_id['a'], w_to_id['b'], w_to_id['c'], w_to_id['d']]
np.random.seed(7)
np.random.shuffle(x_train)
np.random.seed(7)
np.random.shuffle(y_train)
tf.random.set_seed(7)
# 使 x_train 符合 SimpleRNN 输入要求:[送入样本数, 循环核时间展开步数, 每个时间步输入特征个数]。
# 此处整个数据集送入,送入样本数为 len(x_train);输入 4 个字母出结果,循环核时间展开步数为 4; 表示为独热码有 5 个输入特征,每个时间步输入特征个数为 5
x_train = np.reshape(x_train, (len(x_train), 4, 5))
y_train = np.array(y_train)
model = tf.keras.Sequential([SimpleRNN(3),
Dense(5, activation='softmax')
])
#以下省略6.4 编码
独热码:数据量大,过于稀松,映射之间是独立的,没有表现出关联性。
Embedding:是一种单词编码方法,用低维向量实现了编码,这种编码通过神经网络训练优化,能表达出单词之间的相关性。
tf.keras.layers.Embedding(词汇表大小,编码维度)
#编码维度就是用几个数字表达一个单词 入 Embedding 时,x_train 维度:[送入样本数,循环核时间展开步数]
6.3.1 的例子如下:
import numpy as np
import tensorflow as tf
from tensorflow.keras.layers import Dense, SimpleRNN, Embedding
import matplotlib.pyplot as plt
import os
input_word = "abcde"
w_to_id = {'a': 0, 'b': 1, 'c': 2, 'd': 3, 'e': 4} # 单词映射到数值 id 的词典
x_train = [w_to_id['a'], w_to_id['b'], w_to_id['c'], w_to_id['d'], w_to_id['e']]
y_train = [w_to_id['b'], w_to_id['c'], w_to_id['d'], w_to_id['e'], w_to_id['a']]
np.random.seed(7)
np.random.shuffle(x_train)
np.random.seed(7)
np.random.shuffle(y_train)
tf.random.set_seed(7)
# 使 x_train 符合 Embedding 输入要求:[送入样本数, 循环核时间展开步数] ,
# 此处整个数据集送入所以送入,送入样本数为 len(x_train);输入 1 个字母出结果,循环核时间展开步数为 1。
x_train = np.reshape(x_train, (len(x_train), 1))
y_train = np.array(y_train)
model = tf.keras.Sequential([Embedding(5, 2),
SimpleRNN(3),
Dense(5, activation='softmax')
])
model.compile(optimizer=tf.keras.optimizers.Adam(0.01),
loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=False),
metrics=['sparse_categorical_accuracy'])
model.fit(x_train, y_train, batch_size=32, epochs=100])6.3.2 的例子如下:
import numpy as np
import tensorflow as tf
from tensorflow.keras.layers import Dense, SimpleRNN, Embedding
import matplotlib.pyplot as plt
import os
input_word = "abcdefghijklmnopqrstuvwxyz"
w_to_id = {'a': 0, 'b': 1, 'c': 2, 'd': 3, 'e': 4,
'f': 5, 'g': 6, 'h': 7, 'i': 8, 'j': 9,
'k': 10, 'l': 11, 'm': 12, 'n': 13, 'o': 14,
'p': 15, 'q': 16, 'r': 17, 's': 18, 't': 19,
'u': 20, 'v': 21, 'w': 22, 'x': 23, 'y': 24, 'z': 25} # 单词映射到数值 id 的词典
training_set_scaled = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10,
11, 12, 13, 14, 15, 16, 17, 18, 19, 20,
21, 22, 23, 24, 25]
x_train = []
y_train = []
for i in range(4, 26):
x_train.append(training_set_scaled[i - 4:i])
y_train.append(training_set_scaled[i])
np.random.seed(7)
np.random.shuffle(x_train)
np.random.seed(7)
np.random.shuffle(y_train)
tf.random.set_seed(7)
# 使 x_train 符合 Embedding 输入要求:[送入样本数, 循环核时间展开步数] ,
# 此处整个数据集送入所以送入,送入样本数为 len(x_train);输入 4 个字母出结果,循环核时间展开步数为 4。
x_train = np.reshape(x_train, (len(x_train), 4))
y_train = np.array(y_train)
model = tf.keras.Sequential([Embedding(26, 2),
SimpleRNN(10),
Dense(26, activation='softmax')
])
model.compile(optimizer=tf.keras.optimizers.Adam(0.01),
loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=False),
metrics=['sparse_categorical_accuracy'])
model.fit(x_train, y_train, batch_size=32, epochs=100])7. 长短记忆网络 LSTM
传统的 RNN 可以通过记忆体实现短期记忆实现连续数据的预测,但是当连续的数据序列变长时,会使展开时间步变长,在反向传播更新参数时,梯度按照时间步连续相乘,会导致梯度消失,所以 1997 年由 Hochreiter 和 Schmidhuber 等人提出了长短记忆网络LSTM。

TF 描述 LSTM 层:
tf.keras.layers.LSTM(记忆体个数,return_sequences= 是否返回输出)
#示例
model=tf.keras.Sequential([LSTM(80,return_sequences=True),
Dropout(0.2),
LSTM(100),
Dropout(0.2),
Dense(1)
])LSTM 实现股票预测代码:
import numpy as np
import tensorflow as tf
from tensorflow.keras.layers import Dropout, Dense, LSTM
import matplotlib.pyplot as plt
import os
import pandas as pd
from sklearn.preprocessing import MinMaxScaler
from sklearn.metrics import mean_squared_error, mean_absolute_error
import math
maotai = pd.read_csv('./SH600519.csv') # 读取股票文件
training_set = maotai.iloc[0:2426 - 300, 2:3].values # 前 (2426-300=2126) 天的开盘价作为训练集, 表格从 0 开始计数,2:3 是提取 [2:3) 列,前闭后开, 故提取出 C 列开盘价
test_set = maotai.iloc[2426 - 300:, 2:3].values # 后 300 天的开盘价作为测试集
# 归一化
sc = MinMaxScaler(feature_range=(0, 1)) # 定义归一化:归一化到 (0,1) 之间
training_set_scaled = sc.fit_transform(training_set) # 求得训练集的最大值,最小值这些训练集固有的属性,并在训练集上进行归一化
test_set = sc.transform(test_set) # 利用训练集的属性对测试集进行归一化
x_train = []
y_train = []
x_test = []
y_test = []
# 测试集:csv 表格中前 2426-300=2126 天数据
# 利用 for 循环,遍历整个训练集,提取训练集中连续 60 天的开盘价作为输入特征 x_train,第 61 天的数据作为标签,for 循环共构建 2426-300-60=2066 组数据。
for i in range(60, len(training_set_scaled)):
x_train.append(training_set_scaled[i - 60:i, 0])
y_train.append(training_set_scaled[i, 0])
# 对训练集进行打乱
np.random.seed(7)
np.random.shuffle(x_train)
np.random.seed(7)
np.random.shuffle(y_train)
tf.random.set_seed(7)
# 将训练集由 list 格式变为 array 格式
x_train, y_train = np.array(x_train), np.array(y_train)
# 使 x_train 符合 RNN 输入要求:[送入样本数, 循环核时间展开步数, 每个时间步输入特征个数]。
# 此处整个数据集送入,送入样本数为 x_train.shape[0]即 2066 组数据;输入 60 个开盘价,预测出第 61 天的开盘价,循环核时间展开步数为 60; 每个时间步送入的特征是某一天的开盘价,只有 1 个数据,故每个时间步输入特征个数为 1
x_train = np.reshape(x_train, (x_train.shape[0], 60, 1))
# 测试集:csv 表格中后 300 天数据
# 利用 for 循环,遍历整个测试集,提取测试集中连续 60 天的开盘价作为输入特征 x_train,第 61 天的数据作为标签,for 循环共构建 300-60=240 组数据。
for i in range(60, len(test_set)):
x_test.append(test_set[i - 60:i, 0])
y_test.append(test_set[i, 0])
# 测试集变 array 并 reshape 为符合 RNN 输入要求:[送入样本数, 循环核时间展开步数, 每个时间步输入特征个数]
x_test, y_test = np.array(x_test), np.array(y_test)
x_test = np.reshape(x_test, (x_test.shape[0], 60, 1))
model = tf.keras.Sequential([LSTM(80, return_sequences=True),
Dropout(0.2),
LSTM(100),
Dropout(0.2),
Dense(1)
])
model.compile(optimizer=tf.keras.optimizers.Adam(0.001),
loss='mean_squared_error') # 损失函数用均方误差
# 该应用只观测 loss 数值,不观测准确率,所以删去 metrics 选项,一会在每个 epoch 迭代显示时只显示 loss 值
checkpoint_save_path = "./checkpoint/LSTM_stock.ckpt"
if os.path.exists(checkpoint_save_path + '.index'):
print('-------------load the model-----------------')
model.load_weights(checkpoint_save_path)
cp_callback = tf.keras.callbacks.ModelCheckpoint(filepath=checkpoint_save_path,
save_weights_only=True,
save_best_only=True,
monitor='val_loss')
history = model.fit(x_train, y_train, batch_size=64, epochs=50, validation_data=(x_test, y_test), validation_freq=1,
callbacks=[cp_callback])
model.summary()
file = open('./weights.txt', 'w') # 参数提取
for v in model.trainable_variables:
file.write(str(v.name) + '\n')
file.write(str(v.shape) + '\n')
file.write(str(v.numpy()) + '\n')
file.close()
loss = history.history['loss']
val_loss = history.history['val_loss']
plt.plot(loss, label='Training Loss')
plt.plot(val_loss, label='Validation Loss')
plt.title('Training and Validation Loss')
plt.legend()
plt.show()
################## predict ######################
# 测试集输入模型进行预测
predicted_stock_price = model.predict(x_test)
# 对预测数据还原 --- 从(0,1)反归一化到原始范围
predicted_stock_price = sc.inverse_transform(predicted_stock_price)
# 对真实数据还原 --- 从(0,1)反归一化到原始范围
real_stock_price = sc.inverse_transform(test_set[60:])
# 画出真实数据和预测数据的对比曲线
plt.plot(real_stock_price, color='red', label='MaoTai Stock Price')
plt.plot(predicted_stock_price, color='blue', label='Predicted MaoTai Stock Price')
plt.title('MaoTai Stock Price Prediction')
plt.xlabel('Time')
plt.ylabel('MaoTai Stock Price')
plt.legend()
plt.show()
##########evaluate##############
# calculate MSE 均方误差 ---> E[(预测值 - 真实值)^2] (预测值减真实值求平方后求均值)
mse = mean_squared_error(predicted_stock_price, real_stock_price)
# calculate RMSE 均方根误差 --->sqrt[MSE] (对均方误差开方)
rmse = math.sqrt(mean_squared_error(predicted_stock_price, real_stock_price))
# calculate MAE 平均绝对误差 ----->E[| 预测值 - 真实值 |](预测值减真实值求绝对值后求均值)
mae = mean_absolute_error(predicted_stock_price, real_stock_price)
print(' 均方误差: %.6f' % mse)
print(' 均方根误差: %.6f' % rmse)
print(' 平均绝对误差: %.6f' % mae)8. GRU 网络
2014 年 cho 等人简化了 LSTM 网络结构,提出了 GRU 网络。
GRU 使记忆体 ht 融合了长期记忆个短期记忆。

TF 描述 GRU 层:
tf.keras.layers.GRU(记忆体个数,return_sequences= 是否返回输出)
#示例
model=tf.keras.Sequential([GRU(80,return_sequences=True),
Dropout(0.2),
GRU(100),
Dropout(0.2),
Dense(1)
])欢迎各位看官及技术大佬前来交流指导呀,可以邮件至 jqiange@yeah.net